비즈네르 암호
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
비즈네르 암호는 16세기부터 사용된 다중 치환 암호의 한 종류이다. 레온 바티스타 알베르티가 다중 알파벳 암호의 개념을 제시하고, 조반니 바티스타 벨라소가 타불라 렉타를 기반으로 반복되는 키를 사용한 암호를 개발했다. 이 암호는 19세기에 비즈네르에게 잘못 귀속되었으나, 찰스 배비지, 프리드리히 카시스키 등에 의해 해독되었다. 비즈네르 암호는 키의 반복성 때문에 해독될 수 있으며, 키 제거, 카시스키 검사, 프리드먼 검사 등의 해독 방법이 존재한다. 이 암호의 변형으로는 보퍼트 암호, 그롱스펠트 암호, 자동 키 암호 등이 있으며, 러닝 키 암호는 한때 해독 불가능한 것으로 여겨지기도 했다.
더 읽어볼만한 페이지
| 비즈네르 암호 | |
|---|---|
| 개요 | |
| 종류 | 다중 문자 암호 |
| 고안자 | 블레즈 드 비제네르 |
| 처음 고안 | 1586년 |
| 암호 방식 | |
| 암호화 방식 | 덧셈 암호 |
| 복호화 방식 | 뺄셈 암호 |
| 암호 길이 | 가변 |
| 키 길이 | 가변 |
| 암호학적 특징 | |
| 특징 | 간단한 다중 문자 암호 방식 중 하나 키가 반복적으로 사용되어 빈도 분석에 취약 |
| 공격 방법 | 카시키 검사법 |
2. 역사
레온 바티스타 알베르티는 1460년대에 다중 치환식 암호의 원형을 고안했다. 이는 기존의 단일 치환식 암호와 달리 둘 이상의 암호 알파벳을 사용하는 방식이었다. 독일의 수도원장 요하네스 트리테미우스, 이탈리아의 과학자 조반니 포르타, 프랑스의 외교관 블레즈 드 비주넬이 이를 계승하여 발전시켰다. 비주넬은 1586년에 『Le traité des chiffres ou secrète manière d'escrire』(비밀 서기법에 관하여)를 출판하며 최종적인 형태를 완성했다. 비즈네르 암호는 100년 이상에 걸쳐 완성되었지만, 단일 치환식 암호에 비해 암호화 및 복호화가 어렵다는 이유로 한동안 널리 사용되지 않았다.
비즈네르 암호는 '빈도분석법'으로 해독이 거의 불가능하고, 열쇠의 개수가 무궁무진하다는 장점 때문에 '난공불락의 사이퍼'라는 별명을 얻었다. 1854년 찰스 배비지가 비즈네르 암호의 변형을 해독했지만 발표하지 않았고, 카시스키가 암호를 완전히 해독하여 19세기에 그 기술을 발표했지만, 16세기에도 숙련된 암호 해독가들은 가끔씩 암호를 해독할 수 있었다.[10]
미국 남북 전쟁 당시 미합중국 남부 연합은 비즈네르 암호를 사용하기 위해 황동 암호 디스크를 사용했다. 그러나 북부 연합은 정기적으로 남부 연합의 메시지를 해독했으며, 남부 연합은 주로 "맨체스터 블러프", "완전한 승리", "응징이 온다"와 같은 세 가지 키 구문에 의존했다.[15]
메시지와 길이가 같은 완전히 무작위적이고 재사용 불가능한 키를 가진 비즈네르 암호는 이론적으로 깨지지 않는 암호인 원타임 패드가 된다.[16]
2. 1. 초기 발명
1467년경, 이탈리아의 건축가이자 학자인 레온 바티스타 알베르티는 다중 알파벳 암호의 개념을 최초로 제시하고 암호 디스크를 활용했다.[5] 1508년, 독일의 수도원장 요하네스 트리테미우스는 자신의 저서 《폴리그라피아》에서 '타불라 렉타'라는 비즈네르 암호의 핵심 구성 요소를 고안했다.[6][7] 1553년, 이탈리아의 과학자 조반니 바티스타 벨라소는 트리테미우스의 타불라 렉타를 기반으로 반복되는 키를 사용하여 암호 알파벳을 전환하는 방식을 제안했다.[9]2. 2. 비즈네르의 공헌과 오해
1586년, 프랑스의 외교관 블레즈 드 비즈네르는 프랑스의 앙리 3세 궁정에서 자동 키 암호의 일종을 발표했다.[8] 비즈네르의 이름이 붙었지만, 현대에 알려진 비즈네르 암호는 1553년 조반니 바티스타 벨라소가 그의 저서 ''La cifra del Sig. Giovan Battista Bellaso''에서 처음 설명한 암호를 기반으로 한다.[9] 벨라소는 요하네스 트리테미우스의 타불라 렉타를 기반으로 했지만, 매 문자마다 암호 알파벳을 전환하기 위해 반복되는 "암호"(키)를 추가했다.19세기에 벨라소의 암호가 비즈네르에게 잘못 귀속되었고, 이로 인해 '비즈네르 암호'라는 명칭이 굳어졌다. 데이비드 칸은 그의 저서 ''암호 해독가''에서 이러한 잘못된 귀속을 개탄하며, 역사가 "이 중요한 공헌을 무시하고 그와 아무런 관련이 없는 퇴행적이고 기본적인 암호를 그에게 [비즈네르] 이름을 붙였다"고 말했다.[10]
2. 3. 해독과 쇠퇴
비즈네르 암호를 포함한 이전의 모든 암호는 키에 주기성이 있다는 공통적인 약점을 가지고 있었다. 예를 들어 "arm"이라는 키를 사용하면 네 번째와 일곱 번째 문자의 키는 a가 된다. 해독자들은 이 주기성을 이용하여 암호를 해독할 수 있었다.[1] 암호화 방식을 복잡하게 만들어도 키의 주기성 문제는 해결되지 않았다.[1]이 문제를 해결하기 위해 난수를 사용하여 키를 만들고, 키의 길이를 늘리는 방법이 고안되었다.[1] 인력의 한계를 극복하기 위해 암호 처리 기계도 등장했지만, 이러한 기계에서도 키의 길이와 난수성이 중요했다.[1]
현대 암호에서도 키의 난수성은 매우 중요하며, 암호화 알고리즘이 공개되어 있기 때문에 치우친 수를 키로 사용하면 쉽게 해독될 수 있다.[1] 키의 길이는 암호의 안전성을 측정하는 척도가 된다.[1]
3. 원리
비즈네르 암호는 여러 개의 카이사르 암호를 순차적으로 사용하여 암호화 및 복호화를 수행한다. 즉, 알파벳의 각 문자가 특정 개수만큼 이동하는 카이사르 암호의 특징을 이용하되, 이동 값을 하나로 고정하지 않고 키워드에 따라 변화시키는 것이다.[25]
암호화와 복호화를 위해서는 '타불라 렉타', '비즈네르 사각형', '비즈네르 표'라고 불리는 표를 사용한다. 이 표는 알파벳 26자를 26번 반복하여 쓰고, 각 행을 이전 행에서 왼쪽으로 한 칸씩 순환 이동시켜 구성한다. 이렇게 하면 26가지의 서로 다른 카이사르 암호 알파벳이 만들어진다.
예를 들어 'a'를 암호화할 때, 비즈네르 표의 1번 줄에서는 'B', 2번 줄에서는 'C'로 바뀌는데, 이는 카이사르 암호에서 알파벳이 특정 개수만큼 이동하는 것과 같은 원리이다.
3. 1. 비즈네르 표
비즈네르 표는 26개의 알파벳 행으로 구성되며, 각 행은 이전 행에서 한 칸씩 왼쪽으로 순환 이동된 형태이다. 각 행은 서로 다른 카이사르 암호 알파벳에 해당한다.[25] 표의 첫 번째 행은 평문 알파벳, 첫 번째 열은 키 알파벳을 나타낸다.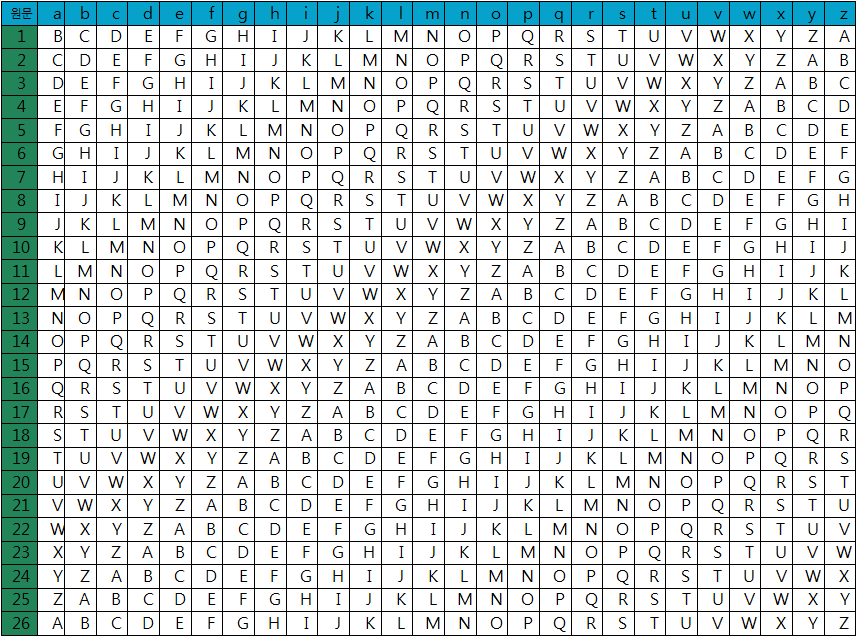
이 표에서 'a'는 1번 줄에서는 'B', 2번 줄에서는 'C' 등으로 바뀌는데, 이는 카이사르 암호에서 알파벳이 특정 개수만큼 이동하는 것과 같은 원리이다.
암호화를 할 때는 이 표를 이용하여 평문의 문자와 키워드의 문자를 번갈아 가며 암호화한다. 예를 들어 평문이 `attackatdawn`이고 키워드가 `LEMON`이면, 평문의 첫 글자 `a`는 키워드의 첫 글자 `L`에 해당하는 행에서 찾고, 두 번째 글자 `t`는 키워드의 두 번째 글자 `E`에 해당하는 행에서 찾는 방식이다.
| 평문: | attackatdawn |
|---|---|
| 키: | LEMONLEMONLE |
| 암호문: | LXFOPVEFRNHR |
복호화는 암호화의 반대 과정으로, 키워드의 문자에 해당하는 행에서 암호문의 문자를 찾고, 그 문자가 위치한 열의 첫 글자를 평문으로 사용한다.
3. 2. 암호화
송신자와 수신자는 사전에 키워드(열쇠)를 정한다. 암호화를 위해 타불라 렉타, ''비즈네르 사각형'' 또는 ''비즈네르 표''라고 불리는 알파벳 표를 사용한다. 이 표에는 알파벳이 26번 반복되어 쓰여 있으며, 각 행은 이전 행과 비교하여 순환적으로 왼쪽으로 이동하여 26가지의 카이사르 암호에 해당한다. 암호화 과정의 여러 지점에서 암호는 여러 행 중 하나의 알파벳을 사용하며, 각 지점에서 사용되는 알파벳은 반복되는 키워드에 따라 달라진다.예를 들어, 평문이 'ATTACKATDAWN'이고 키워드가 'LEMON'이라면, 'L' 행의 'A' 열에 해당하는 'L', 'E' 행의 'T' 열에 해당하는 'X'와 같이 암호화된다. 키워드는 평문의 길이만큼 반복된다. 아래는 그 예시이다.
| 평문: | attackatdawn |
| 키: | LEMONLEMONLE |
| 암호문: | LXFOPVEFRNHR |
오른쪽 그림(비제네르 사각형)을 사용하여 암호화를 수행할 수 있다. 평문을 소문자, 암호문을 대문자로 표시하면, 예를 들어 키를 arm, 평문을 code라고 할 때, 비제네르 사각형에서 a와 c의 교차는 C이고, r과 o는 F, m과 d는 P와 같이 암호문 C, F, P를 얻을 수 있다. 평문이 키보다 긴 경우 키를 반복하여 사용하고, 마지막 평문 e는 a와의 교차로 E가 된다. 즉 평문 "code"는 암호문 "CFPE"가 된다.
3. 3. 복호화
복호화는 암호문의 각 문자에 대해, 키워드의 해당 문자를 사용하여 비즈네르 표에서 평문을 찾는 방식으로 수행된다. 우선 표에서 키에 해당하는 행으로 이동하고, 해당 행에서 암호문 문자의 위치를 찾은 다음, 그 열의 레이블을 평문으로 사용한다.[3] 예를 들어 설명하면 다음과 같다.- 암호문: `LXFOPVEFRNHR`
- 키워드: `LEMON`
1. `LEMON`의 첫 글자 'L' 행에서 암호문 'L'을 찾으면 'A' 열에 해당하므로 첫 번째 평문 문자는 'a'이다.[3]
2. `LEMON`의 두 번째 글자 'E' 행에서 암호문 'X'를 찾으면 'T' 열에 해당하므로 두 번째 평문 문자는 't'이다.[3]
이와 같은 방식으로 나머지 암호문도 복호화할 수 있다.
오른쪽 그림(비즈네르 사각형)을 사용하여 복호화를 수행할 수도 있다. 예를 들어 키가 'arm'이고 암호문이 'CFPE'일 때, 복호화 과정은 다음과 같다.
1. 비즈네르 사각형에서 'a' 행에서 'C'의 위치를 찾고, 거기서 위로 거슬러 올라가면 맨 위 행의 문자는 'c'이므로 평문은 'c'이다.
2. 'r' 행에서 'F'를 찾아 위로 거슬러 올라가면 'o'를 얻는다.
3. 'm' 행에서 'P'를 찾아 위로 거슬러 올라가면 'd'를 얻는다.
4. 평문이 키보다 길 경우 키를 반복하여 사용하므로, 'a' 행에서 'E'를 찾아 위로 거슬러 올라가면 'e'를 얻는다.
따라서 암호문 'CFPE'는 평문 'code'로 복호화된다.
3. 4. 수학적 설명
비즈네르 암호는 모듈러 연산을 사용하여 대수적으로 표현할 수 있다. 먼저, A부터 Z까지의 알파벳을 0부터 25까지의 숫자로 나타낸다. (A=0, B=1, ..., Z=25) 그리고 26으로 나눈 나머지를 구하는 모듈러 연산을 활용한다.암호화 과정은 다음과 같다. 평문의 각 문자를 , 키의 각 문자를 라고 할 때, 암호문 는 다음과 같이 계산된다.
:
즉, 평문의 각 문자에 해당하는 숫자와 키의 각 문자에 해당하는 숫자를 더한 후, 26으로 나눈 나머지를 구하면 암호문의 각 문자에 해당하는 숫자가 된다.
복호화 과정은 다음과 같다. 암호문의 각 문자를 , 키의 각 문자를 라고 할 때, 평문 는 다음과 같이 계산된다.
:
즉, 암호문의 각 문자에 해당하는 숫자에서 키의 각 문자에 해당하는 숫자를 뺀 후, 26으로 나눈 나머지를 구하면 평문의 각 문자에 해당하는 숫자가 된다.
예를 들어, 평문 'T'를 키 'E'로 암호화하는 경우를 생각해보자. T는 19, E는 4에 해당하므로, (19 + 4) mod 26 = 23 이 되고, 23은 X에 해당하므로 암호문은 'X'가 된다. 반대로 암호문 'X'를 키 'E'로 복호화하는 경우, (23 - 4) mod 26 = 19 가 되고, 19는 T에 해당하므로 평문 'T'를 얻을 수 있다.
4. 해독법
비즈네르 암호는 글자 빈도를 숨겨 빈도 분석을 어렵게 만들지만, 키의 반복적인 특성 때문에 해독될 수 있다. 암호 분석가가 키의 길이 ''n''을 정확하게 추측하면, 암호문은 ''n''개의 엇갈린 카이사르 암호로 취급되어 각각 해독될 수 있다. 키 길이는 가능한 모든 ''n'' 값을 무차별 대입하여 테스트하거나, 카시스키 검사 및 프라이드먼 검사를 통해 결정할 수 있다.
키의 길이가 알려지면, 암호문을 키의 각 문자에 해당하는 여러 열로 나눌 수 있다. 각 열은 단일 카이사르 암호로 암호화된 평문으로 구성된다. 카이사르 키(쉬프트)는 해당 열에 사용된 비즈네르 키 문자이다. 카이사르 암호를 해독하는 데 사용되는 방법과 유사하게, 암호문의 각 문자를 해독할 수 있다.
빈도 분석 과정1. 같은 문자의 나열을 찾는다. 문자열이 길수록 좋다.
2. 문자 나열의 간격을 센다.
3. 발견된 문자 간격의 최대공약수를 통해 키의 문자 수를 추정한다.
4. 암호문의 간격이 최대공약수의 값인 문자끼리는 같은 행(단순한 시저 암호)이 사용되었음을 알 수 있다.
5. 암호문의 해당 간격 문자들의 빈도를 그래프로 나타내면 평문의 빈도 분석과 비슷하면서도 다른 형태가 된다.
6. 문자를 약간 이동시켜 평문의 빈도 분석 결과와 거의 같게 만들어 비즈네르 암호를 해독한다.
"반복되는 문자열"은 평문이 같을 때, 같은 비즈네르 격자의 행에 해당하는 부분에서 생성된다. "간격을 센다"는 것은 평문이 같았던 경우, 사용된 키는 그 간격의 약수여야 하기 때문이다. 키의 문자 수를 알면, 이전 방식의 해독법으로 해독할 수 있다는 것이 비즈네르 암호의 가장 큰 결점이다. 시저 암호는 키가 26개뿐이므로 모두 조사할 수 있지만, 비즈네르 암호는 연속된 문자열이 아니므로 모두 조사해도 의미 있는 단어가 되기 어렵다.
비즈네르 암호는 키 길이가 알려져 있거나 추측할 수 있다면 키 제거를 통해서도 해독이 가능하다. 암호문을 키 길이만큼 엇갈리게 자기 자신에서 빼면, 평문을 자기 자신에서 뺀 결과와 같아진다. 이 방법은 평문에 추정 가능한 단어가 있어야 키를 복구할 수 있다는 조건이 있다.
4. 1. 카시스키 검사
1863년 프리드리히 카시스키가 발표한 해독법이다.[18] 카시스키 검사는 카시스키 검정이라고도 하며, 암호문에서 반복되는 문자열을 찾아 그 간격을 통해 키의 길이를 추정한다. 반복되는 문자열은 평문에서 같은 문자가 같은 키 문자에 의해 암호화되었을 때 발생한다.예를 들어, 키워드 `ABCD`를 사용한 다음 암호화를 고려해 볼 수 있다.
키: '''''ABCDAB'''''CDABCDABCD'''''ABCDAB'''''CDABCD
평문: '''''crypto'''''isshortfor'''''crypto'''''graphy
암호문: '''''CSASTP'''''KVSIQUTGQU'''''CSASTP'''''IUAQJB
암호문에서 `CSASTP` 의 반복 사이 거리는 16이다. 반복되는 문자열이 같은 평문 문자열을 나타낸다고 가정하면 키의 길이는 16, 8, 4, 2 또는 1이다. (거리의 모든 인수가 가능한 키 길이다.) 키 길이 2와 1은 비현실적으로 짧으므로, 16, 8, 4의 길이만 시도해야 한다.
다음 암호문에는 두 개의 반복되는 세그먼트가 있다.
암호문: VHVS'''''SP'''QUCE'''''MRVBVBBB'''VHVS'''''URQGIBDUGRNICJ'''QUCE'''''RVUAXSSR
`VHVS`의 반복 사이의 거리는 18이다. 반복되는 세그먼트가 같은 평문 세그먼트를 나타낸다고 가정하면, 키의 길이는 18, 9, 6, 3, 2 또는 1자이다. `QUCE`의 반복 사이의 거리는 30자이다. 즉, 키 길이는 30, 15, 10, 6, 5, 3, 2 또는 1자일 수 있다. 이러한 집합의 교집합을 취함으로써, 3, 2, 1은 비현실적으로 짧으므로 가장 가능성 있는 키 길이는 6임을 안전하게 결론지을 수 있다.
더 긴 메시지는 일반적으로 더 많은 반복되는 암호문 세그먼트를 포함하므로 검정의 정확도가 높아진다. 발견된 문자 간격들의 최대공약수를 통해 키 길이를 유추할 수 있다.
이 해독법을 발견한 사람은 컴퓨터(Computer)의 원형을 만든 찰스 배비지이지만, 여기에도 일화가 있다.
4. 2. 프리드먼 검사 (카파 검사)
1920년대 윌리엄 F. 프리드먼이 개발한 해독법이다.[23] 일치 지수를 이용하여 키의 길이를 추정한다. 이 방법은 임의로 선택한 두 개의 원본 언어 문자가 동일할 확률 (대소문자를 구분하지 않는 영어의 경우 약 0.067)과 알파벳에서 균일하게 무작위로 선택할 때 일치할 확률 (영어의 경우 0.0385)을 비교하여 키 길이를 계산한다.[23]키 길이는 다음 공식을 통해 추정할 수 있다.
:
관측된 일치율()은 다음 공식을 통해 계산한다.
:
여기서
- ''c''는 알파벳의 크기(영어의 경우 26)
- ''N''은 텍스트의 길이
- ''n''1부터 ''n''''c''는 관측된 암호문 문자 빈도를 정수로 나타낸 값
하지만 이는 근사치이며, 정확도는 텍스트 길이에 따라 달라진다. 실제로는 추정치에 가까운 다양한 키 길이를 시도해야 한다.[23] 반복 키 암호의 경우, 가정된 키 길이만큼 열이 있는 행렬에 암호문을 행으로 복사한 다음, 각 열을 개별적으로 고려하여 평균 일치 지수를 계산하는 것이 더 나은 방법이다. 각 가능한 키 길이에 대해 이 작업을 수행하면 가장 높은 평균 일치 지수가 가장 가능성이 높은 키 길이에 해당한다.[24] 이러한 검정은 카시스키 검사의 정보로 보완될 수 있다.
4. 3. 빈도 분석
비즈네르 암호의 기본 원리는 평문의 글자 빈도를 숨겨서 단순한 빈도 분석을 어렵게 만드는 것이다. 예를 들어, 평문이 영어이고 암호문에서 'P'가 가장 자주 나타나는 글자라면, 'P'가 'e'에 해당한다고 추측할 수 있다. (영어에서 'e'가 가장 많이 사용되기 때문) 그러나 비즈네르 암호를 사용하면 'e'는 메시지의 위치에 따라 다른 글자로 암호화될 수 있어 빈도 분석이 효과를 발휘하기 힘들다.하지만 비즈네르 암호는 키가 반복된다는 약점이 있다. 만약 암호 해독가가 키의 길이 ''n''을 알아낸다면, 암호문은 ''n''개의 엇갈린 카이사르 암호로 볼 수 있고, 각각은 쉽게 해독 가능하다. 키 길이는 가능한 모든 ''n'' 값을 무차별 대입하여 찾거나, 카시스키 검사 및 프라이드먼 검사를 통해 알아낼 수 있다.
키의 길이가 알려지면, 암호문을 키의 각 문자에 해당하는 여러 열로 나눌 수 있다. 각 열은 단일 카이사르 암호로 암호화된 평문으로 구성된다. 카이사르 키(쉬프트)는 해당 열에 사용된 비즈네르 키의 문자이다. 카이사르 암호를 해독하는 데 사용되는 방법과 유사하게, 암호문의 각 문자를 해독할 수 있다.
빈도 분석 과정1. 같은 문자의 나열을 찾는다. 문자열이 길수록 좋다.
2. 문자 나열의 간격을 센다.
3. 발견된 문자 간격(예: 9, 63, 180)의 최대공약수(3 또는 9)를 통해 키의 문자 수를 추정한다.
4. 암호문의 간격이 3인 문자끼리는 같은 행(단순한 시저 암호)이 사용되었음을 알 수 있다.
5. 암호문의 3 간격 문자들의 빈도를 그래프로 나타내면 평문의 빈도 분석과 비슷하면서도 다른 형태가 된다.
6. 문자를 약간 이동시켜 평문의 빈도 분석 결과와 거의 같게 만들어 비즈네르 암호를 해독한다.
핵심:
- "반복되는 문자열"은 평문이 같을 때, 같은 비즈네르 격자의 행에 해당하는 부분에서 생성된다.
- "간격을 센다"는 것은 평문이 같았던 경우, 사용된 키는 그 간격의 약수여야 하기 때문이다.
- 키의 문자 수를 알면, 옛날 방식의 해독법으로 해독할 수 있다는 것이 비즈네르 암호의 가장 큰 결점이다.
- 시저 암호는 키가 26개뿐이므로 모두 조사할 수 있지만, 비즈네르 암호는 연속된 문자열이 아니므로 모두 조사해도 의미 있는 단어가 되기 어렵다.
4. 4. 키 제거
비즈네르 암호는 키 길이가 알려져 있거나 추측할 수 있다면 해독이 가능하다. 암호문을 키 길이만큼 엇갈리게 자기 자신에서 빼면, 평문을 자기 자신에서 뺀 결과와 같아진다. 이 방법을 사용하려면 평문에 추정 가능한 단어가 있어야 하며, 이를 통해 키를 복구할 수 있다.예를 들어, 키가 "LION"이고 평문이 "thequickbrownfoxjumpsoverthelazydog"라면, 암호문은 "EPSDFQQXMZCJYNCKUCACDWJRCBVRWINLOWU"가 된다. 여기서 암호문을 키 길이 4만큼 이동하여 자기 자신에서 빼면 다음과 같다.
| 암호문 (원본) | EPSDFQQXMZCJYNCKUCACDWJRCBVRWINLOWU |
| 암호문 (이동) | FQQXMZCJYNCKUCACDWJRCBVRWINLOWU____ |
| 결과 (차이) | ZZCGTROOOMAZELCIRGRLBVOAGTIGIMT |
이는 평문을 같은 만큼 이동하여 자기 자신에서 뺀 것과 거의 같다.
| 평문 (원본) | thequickbrownfoxjumpsoverthelazydog |
| 평문 (이동) | uickbrownfoxjumpsoverthelazydog____ |
| 결과 (차이) | zzcgtrooomazelcirgrlbvoagtigimt |
만약 "brownfox"라는 단어가 평문에 있다고 가정하면, 이 단어를 자기 자신에서 뺀 결과("omaz")를 통해 키의 일부를 유추할 수 있다.
| 평문 (원본) | brownfox |
| 평문 (이동) | nfox____ |
| 결과 (차이) | omaz |
"omaz"는 위의 암호문에서 9번째부터 12번째 문자에 해당한다. 암호문의 해당 범위에서 "brow"를 빼면 키 "LION"을 얻을 수 있다.
| 암호문 | EPSDFQQXMZCJYNCKUCACDWJRCBVRWINLOWU |
| 평문 | ________brow_______________________ |
| 키 | LION |
이러한 키 제거 방법은 특히 짧은 메시지에 유용하다.
다른 예시로, 암호문이 "talsyvbaeifvmssmms"이고, 키가 평문과 같은 길이(18자)이며, 평문이 영어라고 가정해보자. 영어에서 자주 사용되는 "The"를 평문의 첫 세 글자로 가정하면, 키는 "ath"로 시작하는 문자열이 된다. "ath"로 시작하는 단어들을 고려하고, 평문이 의미있는 문자열이 되는 조합을 찾다보면, 키가 "athensparisstlouis"(아테네, 파리, 세인트루이스)이고 평문이 "THEOLDMANANDTHESEA"(『노인과 바다』)임을 유추할 수 있다.
5. 변형
비즈네르 암호에는 여러 가지 변형이 존재한다.
비즈네르 암호는 표에 매우 강한 대칭성(선형성)이 있어 해독의 단서가 된다. 이를 해결하기 위해 표 안의 문자를 무작위로 배치하는 방법이 고안되었다. 이 방법은 카시스키 검사의 유효성을 현저히 감소시켜 종이와 펜만으로는 거의 해독할 수 없게 만들었다. 하지만 표 작성과 해독에 시간이 오래 걸리고, 비즈네르 암호가 해독 불가능하다고 여겨졌기 때문에 널리 사용되지는 않았다. 무작위 배치 방식은 현대 암호에서 S-box 구현에 활용되어 선형 해독법, 차분 해독법에 대한 내성을 강화한다.
비즈네르 자신이 1586년에 발표한 무작위 배치 표는 '비즈네르 표'라고 불리지는 않는다. 무작위 배치는 해독을 어렵게 만들지만, 확률론적으로 취약한 표가 만들어질 수 있으므로 취약성 검정이 필요하다.
5. 1. 러닝 키 암호
비즈네르 암호의 러닝 키 변형은 한때 해독 불가능한 것으로 여겨지기도 했다. 이 방법에서는 평문과 길이가 같은 텍스트 블록을 키로 사용한다. 키가 메시지와 길이가 같기 때문에 키가 반복되지 않으므로 프리드먼 검정과 카시스키 검정이 더 이상 작동하지 않는다.[1]여러 개의 키를 사용하는 경우, 실질적인 키 길이는 개별 키 길이의 최소공배수가 된다. 예를 들어, 길이가 각각 2와 3인 `GO`와 `CAT`이라는 두 개의 키를 사용하면 실질적인 키 길이는 6(2와 3의 최소공배수)이 된다. 이는 두 키가 모두 일치하는 지점으로 이해할 수 있다.[1]
| 평문 | attackatdawn |
|---|---|
| 키 1 | GOGOGOGOGOGO |
| 키 2 | CATCATCATCAT |
| 암호문 | IHSQIRIHCQCU |
먼저 `GO` 키로 암호화한 다음 `CAT` 키로 다시 암호화하는 것은 하나의 키를 다른 키로 암호화하여 생성된 키로 한 번 암호화하는 것과 같다.[1]
| 평문 | gogogo |
|---|---|
| 키 | CATCAT |
| 암호문 | IOZQGH |
이는 `attackatdawn`을 `IOZQGH`로 암호화하여 원래 예제와 같은 암호문을 생성하는 것으로 보여준다.[1]
| 평문 | attackatdawn |
|---|---|
| 키 | IOZQGHIOZQGH |
| 암호문 | IHSQIRIHCQCU |
키 길이가 서로소이면 개별 키 길이가 증가함에 따라 실질적인 키 길이는 기하급수적으로 증가한다. 예를 들어, 10, 12, 15자 길이의 키의 실질적인 길이는 60에 불과하지만, 8, 11, 15자 길이의 키의 실질적인 길이는 1320이다. 이 실질적인 키 길이가 암호문보다 길면 러닝 키 변형과 마찬가지로 프리드먼 검정과 카시스키 검정에 대한 면역성을 갖게 된다.[1]
진정으로 무작위적인 키를 사용하고, 암호화된 메시지보다 길이가 같거나 더 길며, 한 번만 사용하는 경우 비즈네르 암호는 이론적으로 해독 불가능하다. 그러나 이 경우에는 암호가 아니라 키가 암호화 강도를 제공하며, 이러한 시스템은 사용된 암호와 관계없이 원타임 패드 시스템으로 통칭된다.[1]
5. 2. 보퍼트 암호
프랜시스 보퍼트가 고안한 보퍼트 암호는 비즈네르 암호와 유사하지만 약간 수정된 암호화 메커니즘과 표를 사용한다. 보퍼트 암호는 상호 암호이다.5. 3. 그롱스펠트 암호
그롱스펠트 암호는 가스파르 쇼트(Gaspar Schott)가 그롱스펠트 백작(요세 막시밀리안 판 그롱스펠트 né van Bronckhorst)에게 귀속시킨 변형이지만, 사실 1560년대~1570년대에 맨투아 공작의 대사가 훨씬 이전에 사용했다. 이 암호는 0부터 9까지의 숫자에 해당하는 10가지의 서로 다른 암호 알파벳만을 사용한다는 점을 제외하면 비즈네르 암호와 동일하다. 0123의 그롱스펠트 키는 ABCD의 비즈네르 키와 같다. 그롱스펠트 암호는 키가 단어가 아니라는 점에서 강화되었지만, 10가지의 암호 알파벳만 사용한다는 점에서 약화되었다. 그럼에도 불구하고 그롱스펠트 암호는 그 약점에도 불구하고 독일과 유럽 전역에서 널리 사용되었다.5. 4. 자동 키 암호
비즈네르가 실제로 발명한 암호는 자동 키 암호이다. 하지만 '비즈네르 암호'라는 이름은 더 간단한 다중 알파벳 암호에 붙여졌다. 두 암호는 종종 혼동되었고, 둘 다 때때로 ''le chiffre indéchiffrable''(해독 불가능한 암호)라고 불렸다.[1] 배비지는 자동 키 암호를 해독했지만, 카시스키가 고정 키 다중 알파벳 암호에 대한 최초의 해결책을 발표한 사람으로 일반적으로 인정받고 있다.[1]참조
[1]
서적
Cryptography, Information Theory, and Error-Correction: A handbook for the 21st Century
https://books.google[...]
John Wiley & Sons
[2]
서적
Everyday Cryptography
https://books.google[...]
Oxford University Press
[3]
서적
Cryptography: The Science of Secret Writing
https://books.google[...]
Courier Corporation
[4]
간행물
Vigenère Cipher
https://crypto.inter[...]
Crypto Corner
[5]
서적
Würzburger Humanismus
Narr Verlag
2015
[6]
서적
Polygraphiae, libri sex …
http://lcweb2.loc.go[...]
Johann Haselberg
1518
[7]
문서
https://www.digitale[...]
[8]
서적
Traicté des Chiffres, ou Secretes Manieres d'Escrire
http://gallica.bnf.f[...]
Abel l'Angelier
1586
[9]
서적
La Cifra del Sig. Giovan Battista Belaso …
https://bibdig.museo[...]
1553
[10]
서적
The Codebreakers: The Story of Secret Writing
Simon & Schuster
[11]
학술지
A new cipher code
https://babel.hathit[...]
1917-01-27
[11]
학술지
Letter to the Editor: Cipher codes
https://babel.hathit[...]
1917-03-03
[11]
학술지
Letter to the Editor: A new cipher
https://babel.hathit[...]
1917-04-14
[11]
학술지
The ciphers of Porta and Vigenère: The original undecipherable code, and how to decipher it
https://babel.hathit[...]
1921-10-01
[12]
서적
State of the Art in Applied Cryptography: Course on Computer Security and Industrial Cryptograph Leuven Belgium, June 1997 Revised Lectures
https://archive.org/[...]
Springer
[13]
서적
The Code Book
Anchor Books, Random House
[14]
웹사이트
Codes, Ciphers, & Codebreaking
http://www.vectorsit[...]
[15]
서적
The Codebreakers: The Story of Secret Writing
Simon & Schuster
[16]
웹사이트
Crypto Overview, Perfect Secrecy, One-time Pad
http://www.ics.uci.e[...]
2004-09-28
[17]
간행물
Vernam-Vigenère cipher
https://www.britanni[...]
Encyclopedia Britannica
[18]
서적
Die Geheimschriften und die Dechiffrir-Kunst
https://books.google[...]
E.S. Mittler und Sohn
1863
[19]
학술지
Secret, or cypher writing
https://books.google[...]
1854-08-11
[19]
학술지
Mr. Thwaites's cypher
https://books.google[...]
1854-09-01
[19]
서적
Passages from the Life of a Philosopher
https://archive.org/[...]
Longman
1864
[20]
웹사이트
Weekly list of patents sealed. … 1727. John Hall Brock Thwaites, Bristol – Improvements in apparatus to facilitate communication by cypher.
https://babel.hathit[...]
[20]
서적
Thwaites, John Hall Brock, of Bristol, dentist. ''Improvements in apparatus to facilitate the communication by cypher''. Application dated August 7, 1854. (No. 1727).
https://books.google[...]
The Mechanics' Magazine
1855-03-03
[21]
학술지
Secret or cypher writing
https://babel.hathit[...]
1854-09-15
[21]
학술지
Mr. Thwaites's cypher
https://babel.hathit[...]
1854-10-06
[22]
서적
Mr. Babbage's Secret: The Tale of a Cypher and APL
https://books.google[...]
Prentice Hall
[23]
서적
Encyclopedia of Cryptography and Security
https://archive.org/[...]
Springer
[24]
학술지
The Bar Statistics
[25]
웹사이트
Lab exercise: Vigenere, RSA, DES, and Authentication Protocols
http://courses.umass[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
